When it comes to evaluating investments, the array of metrics can feel overwhelming. Terms like CAGR, XIRR, and Absolute Returns are commonly used to measure performance, but their meanings and applications are often misunderstood. Each metric provides valuable insights, but using the wrong one could lead to an inaccurate assessment of your investment’s success.

This article unpacks the distinctions between these terms in simple, relatable language, helping you understand when and why to use them. Whether you are analysing a mutual fund’s growth, comparing investment options, or tracking returns with cash flow variations, this guide will empower you to make informed financial decisions.

– Absolute Returns

The absolute return of an investment is a type of investment metric wherein the gain on an investment is measured based on the difference between its market price and initial investment amount. It is the percentage gain on investment in the nature of capital appreciation. Typically, it is calculated as follows:

Absolute Return (%) = (Market Value – Invested Amount)/ Invested Amount*100

Illustration:

Mr. A buys 1500 shares of a company at Rs. 300 each. After a period of 3 years, the market price of the shares increases to Rs. 500 on the stock exchange. Mr. A wants to know his return on investment made 3 years ago in order to decide if he should keep holding the stock or craft a new investment strategy.

Mr. A’s Absolute Return (%) = ((1500*500) – (1500*300)/(1500*300))*100 = 66.67%.

This is a simple and easy to understand way of calculating investment returns. However, this method has some deficiencies:

1. Absolute return does not consider the time period over which the return is generated, making it less informative for investments held over different time horizons. This makes it less suitable for calculating returns for cashflows over a long-time horizon, as compared to methods such as CAGR and XIRR.

2. The Market Value reflects the cumulative effect of the initial investment’s growth or loss, plus the reinvested cash flows (e.g., dividends or interest). If these cash flows are not reinvested, it will not appear in the Market Value, as it remains separate from the principal and hence absolute return does not separately track cash flows like dividends or interest unless reinvested and reflected in the Market Value.

– CAGR

CAGR, short for Compound Annual Growth Rate, is a metric which measures the annualized growth rate of an investment over a specific time period, assuming that the profits from the investment are reinvested at the end of each year. CAGR is calculated as follows:

CAGR = (Market Value/ Invested Amount)^1/n – 1

Here, n is the period of the investment. If n is taken as the number of years, CAGR will be calculated as a yearly rate. It will be a monthly rate if n is taken as number of months, etc.

Let us understand this better with our previous example:

CAGR = ((1500*500)/(1500*300))^1/3 -1 =18.56% per annum.

Hence, from the above calculations we can conclude that Mr. A effectively earned a compounded return of 18.56% per annum, assuming that the gains were reinvested at the end of each year.

The key difference in this case vs Absolute Return is the fact that gains are assumed to reinvested at each year end in CAGR, whereas no such assumption is made in absolute returns. This means that mathematically in order to arrive at Rs. 500 from the initial investment of Rs. 300 per share:

• In case of Absolute Return: –

• In case of CAGR: –

Limitations of CAGR:

1. It does not account for additional cashflows in between the period, such as additional investment or receipt of dividends, etc. Hence, it is less suitable than a metric like XIRR for measurement of returns on investments in the nature of SIPs, etc.

2. CAGR assumes that the growth happens evenly year-over-year due to compounding, even though actual growth might vary within the period. This makes it a smoothed rate, ideal for comparisons but not a reflection of real-world volatility.

– XIRR

XIRR (Extended Internal Rate of Return) calculates the annualized return of an investment, accounting for regular as well as irregular cash flows (e.g., investments, withdrawals, dividends) at specific dates. Unlike CAGR, which assumes a single lump sum investment and uniform time periods, XIRR accounts for the exact dates and amounts of cash flows, making it more accurate for real-world scenarios.

XIRR does not have a direct formula but is calculated based on guessing of rate which satisfies the following equation:

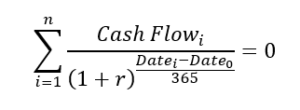
Let us understand this with another Illustration:

Suppose Mr. A, instead of investing lumpsum decides to invest and withdraw the same amount in shares but at irregular intervals in the 3 years. Snapshot of his demat account:

Substituting the values in the above equation, we get:

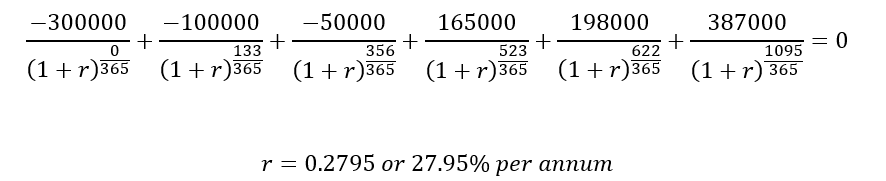
XIRR for this type of scenario can be more easily calculated using software-based calculators.

In Microsoft Excel, XIRR can be calculated using the XIRR function.

=XIRR(values,dates,[guess])

Where,

“values” is the range of cash flows and,

“dates” is the range of corresponding dates.

Hence, it is important to note that just a change in the timing of cashflows will give a different annualized rate of return for the same amount of total investment, final amount, and tenure of the investment. Practically, XIRR is regarded as one of the most accurate measures for rate of return on investment and is widely used for tracking portfolio performances. However, metrics like CAGR and Absolute Return are also useful for the scenarios discussed earlier and give a good understanding of the overall performance of the investment.

Limitations of XIRR:

1. XIRR requires financial tools like Excel or software since the calculations are more complex and involves iterative computations.

2. It is sensitive to the dates of the cashflows and just a small error in one or more dates can impact the final output easily.

Conclusion:

Each performance metric – CAGR, XIRR, and Absolute Returns has its strengths, and understanding their differences is crucial for making better investment decisions. Knowing when to use each metric helps provide a clearer picture of investment growth. To truly understand how an investment is performing, it’s vital to choose the method that best matches the specific cash flow structure of the investment.

Using a combination of these measures, rather than relying on one alone, will give investors a more complete and accurate understanding of their portfolio’s performance, helping them optimize their strategies and make more informed decisions towards their financial goals. 

To understand more on the topic as well as to start investments please feel free to contact us:

Phone: +91-9324609115

E-mail: team@richvikwealth.in

The article is authored by Mr. Aditya Nembhwani from Team RichVik.